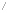타원곡선암호

타원 곡선의 그래프

타원곡선암호(ECC; Elliptic Curve Cryptography)는 타원곡선을 기반으로 한 암호방식으로, 대표적인 공개키 방식 중 하나이다. 타원곡선암호 기술은 기존 RSA 암호방식에 대한 대안으로 1985년도에 제안된 방식이다. 비트코인이 타원곡선암호 기술 방식에 속하는 타원곡선 디지털서명 알고리즘(ECDSA; Elliptic Curve Digital Signature Algorithm) 암호 알고리즘을 사용하고 있다. 타원곡선암호는 타원곡선 암호화 알고리즘이라고도 부른다.

개요

타원곡선암호는 타원곡선 이론에 기반한 공개키 암호 방식이다. 1985년, 워싱턴대학교의 수학교수인 닐 코블리츠(Neal Koblitz)와 IBM연구소의 빅터 밀러(Victor Miller)가 거의 동시에 독립적으로 고안한 개념으로, 아직 그 해독 방법은 발견되지 않았다. 타원곡선 군의 연산에서 정의되는 이산대수 문제의 어려움의 이용을 기초로 하는 공개키 암호 알고리즘 시스템으로서 RSA/DSA와 같은 공개키 암호보다 짧은 키 길이와 빠른 연산속도를 가지면서 동일한 수준의 보안 강도를 제공한다. 보안을 강화하기 위해서 암호키의 길이를 늘이는 방법이 있지만, 그에 따라 암호 연산 속도가 느려진다는 문제가 있다. 그래서 사람들은 RSA 방식을 사용하여 암호키 길이를 늘이는 대신 타원곡선암호 기술을 선택하는 경우가 많다.

타원곡선암호는 유한체 상의 타원곡선의 수학적 성질을 이용한 암호 기술을 이야기한다. 공개키 암호화 방식 중 하나인 타원곡선암호는 이러한 유한체 위에서의 타원곡선의 대수적 구조를 기반으로 한 이산로그 문제에 착안해서 만들어졌다. 여기서 유한체란 집합에 속해 있는 원소의 수가 한정되어 있으며, 덧셈과 곱셈 연산에 대해서 닫혀 있는 집합을 말하는데, 닫혀 있다는 말은 곧 연산의 결괏값도 집합에 속해있음을 의미한다. 암호학에서는 그래프와 부딪히는 값을 추측하지 못하도록 더 어렵게 하기 위해, 정의역과 치역을 소수 p 체계로 한정한다. 암호화 애플리케이션은 빠르고 정확한 산술 연산이 필요하다. 유한체는 컴퓨터 계산에 매우 적합하기 때문에 타원 곡선에 사용되며, 타원곡선암호의 p를 가지고 모듈러 계산을 하는데 이는 유한체이다. 또, 타원곡선이 암호학에 적합한 이유는 실수 상에서 연산하든, 유한체 상에서 연산하든 언제나 동일한 수학 법칙이 적용되기 때문이고, 암호 연산은 정수를 기반으로 계산해야 하기 때문이다.

타원 곡선의 방정식은 $y^{2}=x^{3}+ax+b$로 표현할 수 있으며 타원곡선 암호화를 통해 $10^{77}$ 정도의 경우의 수를 얻을 수 있다.

RSA는 1024비트를 사용하는 반면에 타원곡선암호는 160비트를 사용하는데, 기존의 공개키 암호보다 적은 비트를 사용하는데도 동일한 안전성을 보장한다. 또한, 암호화 처리 속도가 매우 빨라서 키 관리에 용이하기 때문에 채택률이 상승했다. 예를 들어 서명할 때 고속 계산을 할 수 있어서 스마트카드 등의 정보처리능력이 그다지 높지 않은 기기에서 사용되기에 적합하다. 현재는 주로 비트코인의 소유권 증명, 미국 정보의 내부 통신 보호, 애플 서비스의 DNS 정보 암호화 등등에 사용되고 있다. 사물인터넷의 경량 암호화로 인해 한동안 주목을 받았으며, 간편결제 인증에서도 사용된 사례가 있다. 그러나 일부 곡선에서는 약점이 발견되는 사례가 몇몇 있기 때문에 실제로 방식을 도입할 때는 이러한 약점들을 피할 수 있는 연구가 함께 병행되어야 한다.

개념

타원곡선의 정의

대체로 사용되는 타원곡선 방정식은 다음과 같은 형태의 3차 방정식이다.

$y^{2}+b_{1}xy+b_{2}y=x^{3}+a_{1}x^{2}+a_{2}x+a_{3}$

그러나 실수 상의 타원 곡선은 다음과 같은 특별한 범주 내의 타원 곡선을 이용한다.

$y^{2}=x^{3}+ax+b$

타원곡선은 일반적으로 타원 형태의 그래프를 생각하는 편이 더 쉽지만, 타원곡선 $y^{2}=x^{3}+ax+b$ 그래프의 곡선은 a와 b 각각의 값에 따라 다양한 형태의 타원 곡선을 정의할 수 있다. x축을 중심으로 대칭이 되는 구조이며, 비 수직선에 대해 최대 3개의 지점에서 곡선과 교차한다는 특징이 있다. 집합 형태는 다음과 같다.

$E(F_{P})=\left\{(x,y)|y^{2}=x^{3}+ax+b\right\}\cup \left\{O\right\}$

타원곡선상에서의 연산

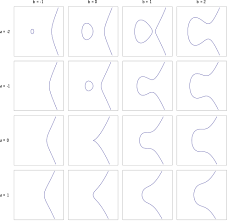
타원 곡선을 이용한 암호화를 이해하기 위해서는 타원곡선 상의 덧셈 연산부터 이해를 해야 한다. 따라서 기하학적으로 설명하자면 다음과 같다. 타원곡선 상의 P와 Q의 덧셈 연산은 점 P와 Q를 지나는 직선이 타원과 만나는 제3의 교점을 x축으로 대칭 시킨 점을 P+Q=R로 정의한다. P와 Q가 같은 경우에는 P+P 연산이 되므로 P 점에서 접선을 그었을 때 타원과 만나는 제3의 교점을 x축으로 대칭 시킨 점에 해당한다. 또한, 무한대 값 0이 가능하고, P+(-P)=0 으로 P와 x축 -P가 덧셈한 결괏값은 무한대 값이다.

타원곡선의 이산로그 문제에 기반한 타원곡선 암호화

타원곡선 암호의 원리 및 키생성

타원곡선 암호는 타원곡선 위의 이산로그 문제가 어렵다는 사실을 이용한 공개키 암호 방식을 말한다. 이러한 타원곡선 암호화를 위한 타원곡선은 임의의 정수 a, b에 대해 정의된 다음과 같은 방정식의 해 (X, Y)의 집합이다.

$Y^{2}=X^{3}+aX+b({\bmod {\,}}p)$

점 P=(x, y)가 타원곡선 상에 있다는 것은 위의 방정식을 만족시킨다는 의미이다. 또한, 두 점 P, Q와 임의의 정수 x에 대해서 다음과 같은 방정식을 정의할 수 있다.

$Q=xG$

타원곡선 이산대수 문제는 바로 위와 같은 상황에서 해 x를 구하는 것이다. 이로부터 타원곡선 암호에서 사용하는 키 쌍은 다음과 같이 정의할 수 있다.

• G: 생성자, 임의의 시작 포인트이다.
• x: 개인키, P보다 적은 소수로, 난수 생성기로 생성했다.
• Q: 공개키, 개인키로부터 연산한다.

이때의 공개키 Q의 경우, Q = x*G = G+G+...G(x번 덧셈)으로 G를 x번 더한 결괏값이다. Q = xG 수식에서 x와 G를 이용하여 Q를 구하기는 쉽지만, G와 Q를 안다고 해서, x의 값을 유추해내는 것은 상당히 어려운 타원곡선 이산대수 문제를 이용한다. G는 타원곡선 상의 임의의 점이며, x*G는 G를 타원곡선상에서 x번 덧셈 연산한 것을 의미한다. 다음은 x*G 연산 과정을 기하학적으로 도식화한 자료이다.

앞에서 설명한 타원곡선 상의 덧셈 연산의 P+P 연산으로 다시 돌아가 살펴보면, 2G=G+G는 점 G에서의 접선이 타원곡선과 만나는 제3의 점을 x축으로 대칭 시킨 지점이다. 4G=2G+2G에 해당하는 점에서도 마찬가지로 접선을 그어 타원 곡선과 만나는 점의 x축 대칭점에 위치한다. G의 상수 배 연산은 이를 계속 반복해서 표현할 수 있고, 이는 타원곡선 상에서 일어나는 특성을 보여준다. 타원곡선은 공개키 암호 체계를 수학적으로 진행하는 한 가지 방법으로 타원곡선을 이용해서 RSA, 엘가말(ElGamal), 디피-헬먼(Diffie-Hellman)의 구현이 가능하다.

타원곡선을 이용한 디피-헬먼

타원곡선 디피-헬먼은 타원곡선에 디피-헬먼 키 교환을 적용한 방법이다. 디피-헬먼 키 교환의 핵심은 서로 통신하는 송수신 자가 서로 같은 키를 공유하는 방법이다. 송수신 자를 각각 앨리스와 밥이라고 가정하자. 앨리스와 밥은 각각 개인키로 $d_{A}$와 $d_{B}$를 선택한다. 그리고 타원곡선 덧셈 연산을 통해서 계산한 $H_{A}$와 $H_{B}$를 서로 교환한다. 그러면 앨리스는 밥으로부터 받은 $H_{B}$에 개인키 $d_{A}$를 타원곡선 덧셈 연산해서 비밀키 S를 생성한다. 반대로 밥 또한 앨리스로부터 받은 $H_{A}$에 개인키 $d_{B}$를 카원곡선 덧셈 연산을 통해서 앨리스와 같은 비밀키 S를 생성한다. 따라서 앨리스와 밥은 별도의 비밀키 교환 없이 위와 같은 방식으로 서로 같은 비밀키를 공유할 수 있다.

타원곡선을 이용한 엘가말

밥은 개인키 d를 생성한 후, 개인키 d로부터 타원곡선 상에서 계산된 공개키 $e_{2}$를 앨리스에게 전달한다. 앨리스는 평문 P를 밥의 공개키를 이용하여$\left(C_{1},C_{2}\right)$ 암호문을 생성해서 밥에게 전달하면, 밥은 밥의 개인키 d를 이용해서 평문 P를 복호화한다. 이 과정에서 암호화와 복호화를 진행할 때 사용되는 곱셈 연산은 앞에서 설명한 타원곡선 덧셈 연산 방식을 이용한다. 이산대수 기반의 엘가말과 타원곡선을 이용한 엘가말의 키 생성, 암호화, 복호화 방식을 비교하자면 다음과 같다. 참고로 다음 중 $x'$은 임의의 난수이다.

	엘가말 공개키 암호	타원곡선 공개키 암호
공개키	$(g,p,y=g^{x}\,{\bmod {\,}}p)$	$(G,p,Y=xG)$
개인키	$(x)$	$(x)$
암호화	$(c_{1},c_{2})=(g^{x}\,{\bmod {\,}}p,y^{x}m\,{\bmod {\,}}p)$	$(C_{1},C_{2})=(x'G,x'Y+M)$
복호화	$c_{2}c_{1}^{-x}\,{\bmod {\,}}p$	$C_{2}-xC_{1}$

특징

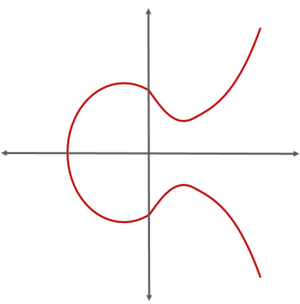
타원곡선암호의 방정식에 ${\pmod {\ }}p$하면 $y^{2}$의 값은 0에서 p-1이다. 정수만 사용하기 때문에 제곱수는 작은 그룹이며, 가능한 점들의 개수는 N이라고 가정한다. 여기서 N의 값은 p보다 작다. 어떤 x 좌표에 대해서든 두 점을 가지기 때문에, 가능한 x 좌표는 ${\frac {N}{2}}$개이다. 즉, 이 타원곡선은 정수계산과 모듈러 때문에 유한한 수의 점을 갖고 있다. 이렇게 바뀐 타원곡선함수는 곡선이 아니라 점들이 뭉쳐 있어 구름처럼 보인다. 암호학에서는 타원곡선의 난도를 높이기 위해 곡선에 부딪히는 횟수도 소수 단위로 한정한다. 또, 일정한 한계치 값을 넘치면 새로운 값에서 함수를 시작하는 등의 제약을 도입하는데, 이렇게 추가로 암호화를 적용한 값은 해독하기가 매우 어렵다. 예를들어, 다음과 같은 수식을 갖는 타원곡선암호가 있다고 가정한다.

$E:y^{2}=x^{3}+x$ $over$ $Z_{23}(p=23)$

만약 여기서 $x=9$라고 한다면, $y^{2}{\pmod {\ }}23=(729+9){\pmod {\ }}23=2$이다. 이때 만족하는 $y$는 $5*{\pmod {\ }}23=2$이므로 $y$는 5가 될 수 있다. 이때 갈루아 필드의 p가 조금만 더 커지면 우리는 y를 쉽게 찾을 수 없다. 따라서 이를 이용하여 암호학에 적용할 수 있다.

타원곡선암호를 사용하기 용이한 경우는 다음과 같다.

• 계산 능력이 제한적일 때 (무선 장치, PC 카드)
• 집적 회로 공간이 제한될 때 (무선 장치, PC 카드)
• 빠른 속도를 필요로 할 때
• 서명, 검증 또는 인증이 필요할 때
• 서명 된 메시지를 저장하거나 전송 할 때 (특히 짧은 메시지의 경우)
• 대역폭이 제한될 때 (무선 통신 및 일부 컴퓨터 네트워크

공개키 알고리즘

공개키 암호 알고리즘(public key cryptosystem) 또는 비대칭키 암호 알고리즘이란 개인이 비밀통신을 할 경우엔 대칭키 암호를 사용할 수 있지만, 다수가 통신할 때에는 키의 개수가 급증하게 되어 큰 어려움이 따른다. 이런 어려움을 극복하기 위해 나타난 것이 공개키 암호이다. 공개키 암호는 다른 유저와 키를 공유하지 않더라도 암호를 통한 안전한 통신을 할 수 있다는 장점이 있다.

공개키 알고리즘은 서로 다른 키를 가지고 있으며 키의 이름은 공개키(Public Key)와 비밀키(Private Key)이다. 이 공개키와 비밀키를 만드는 알고리즘인 공개키 알고리즘은 두 가지 방식으로 분류할 수 있다. 소인수분해 문제를 이용해서 만드는 방법과 이산 로그 문제를 이용해서 만드는 방법이 있다. RSA는 소인수분해 문제를 선택하고 있다면 타원곡선 암호는 이산 로그 문제를 사용하고 있다.

난수 생성기의 중요성

RSA에 비교한 타원곡선암호의 약점은 사용되는 프라이빗 키의 비트 수가 적다는 것이다. 프라이빗 키는 난수 생성기를 통해서 만들어지기 때문에 난이도가 낮다면 공격자에 의해 프라이빗 키가 예측될 위험이 존재한다. 타원곡선을 이용한 전자서명 알고리즘인 ECDSA 암호 알고리즘의 보안성은 사용되는 개인키의 보안성에 의해 좌우 된다. 그렇기 때문에 예측할 수 없는 난수를 가진 개인 키를 생성해야 한다.

국제표준화 동향

각종 국제표준들에서 타원곡선암호에 대한 표준화가 활발히 진행되고 있고 실제로 다양한 응용 분야에서 타원곡선암호를 지원하고 있다. 표준화는 여러 가지의 다른 H/W와 S/W와의 상호운용성(interoperability)을 보장하고, 암호학적 관점에서 시스템의 안전도를 면밀하게 재검토할 수 있으며, 다양하고 폭넓은 환경에서 시스템을 구현하는 설계자들에게 암호 시스템을 설계할 수 있도록 도와주는 역할을 한다. 현재의 표준화는 타원곡선암호의 구현을 위한 많은 표준의 차이로 인해 서로 다르게 구현된 응용 사이에서의 호환성 문제가 대두됨에 따라 상호운용적인 보안솔루션의 개발 및 적용 시 사용자가 직면하는 문제점을 해결하기 위한 표준제정이라는 추세를 보이고 있다. 캐나다의 써티콤이 설립한 SECG(Standards for Efficient Cryptography Group)는 다양한 암호 솔루션 간에 발생하는 상호운용성의 해결, 각 솔루션에 타원곡선암호의 효과적인 편입, 스마트카드나 PDA 같은 제한적인 환경에서뿐만 아니라 일반적인 공개키 기반구조에 타원곡선암호가 널리 적용되도록 하기위한 표준화 정보제공 등을 목표로, SEC 1에서는 ECDSA(Elliptic Curve Digital Signature Algorithm: 미국연방표준 전자서명 알고리즘 DSA를 타원곡선을 이용하여 변형한 전자서명), ECDH(Elliptic Curve Diffie-Hellman: 타원곡선을 이용한 키 합의 프로토콜) 등을 포함하고, 선택사항에 대해서는 제약을 두어 여러 표준들 사이에 호환성을 높이고 있으며 SEC 2에서는 유한체의 크기마다 널리 쓰이는 권장 타원곡선 도메인 변수들의 선정기준을 제시하고 있다.

안정성

타원곡선 이산로그에서는 인수분해나 유한체의 이산로그와는 달리 현재까지 알려진 적용 가능한 준지수시간 알고리즘이 존재하지 않고 Pollard-rho 알고리즘을 병렬화시킨 방법이 타원곡선 이산대수 문제를 푸는 가장 효율적인 알고리즘으로 알려져 있다. 이러한 알고리즘들을 피해 타원곡선암호를 안전하게 사용하기 위해서는 약 160비트 이상의 유한체에서 정의된 타원곡선을 사용해야 하며 취약성이 알려진 초특이곡선과 비정규곡선 및 트레이스가 2인 곡선은 반드시 피해야만 한다. 아래 표는 써티콤이 제시한 자료로서 RSA/DSA와 타원곡선에 대한 도메인 변수의 크기를 비교한 것이다. 이 표는 타원곡선암호의 안전도가 키 길이의 증가에 따라 거의 지수 함수적으로 증가하고 있고, 기존의 공개키 암호 시스템에 비해 장기적인 기술의 발전에 따른 키 길이의 증가 비율 면에서도 대단한 장점을 가지고 있음을 확인할 수 있게 해 준다.

동일한 안전도를 갖는 도메인 변수들의 크기 비교

Time to break in MIPS(Million Instrucion Per Second) year	RSA/DSA (bits)	ECC (bits)	RSA vs. ECC key size ratio
$10^{4}$	512	106	5:1
$10^{8}$	768	132	6:1
$10^{11}$	1024	160	7:1
$10^{20}$	2048	210	10:1
$10^{78}$	21000	600	35:1

• RSA

타원곡선암호를 RSA와 비교하면 타원곡선암호가 RSA보다 더 짧은 키를 사용하지만, 안전성 면에서는 RSA와 비슷한 수준을 제공한다. 타원곡선 암호화의 160비트 키 길이의 암호 강도는 이산대수의 특징을 이용한 비대칭키 알고리즘인 RSA 1024 길이의 키 강도와 맞먹는다. 키 값이 점점 커질수록 암호화 레벨은 RSA의 레벨보다 급격하게 상승한다. 타원곡선 암호화 방식은 더 적은 비트로도 동일한 안전성을 얻을 수도 있다. 그러나 단점은 RSA보다 연산이 더 복잡하다는 점이다.

RSA와 타원곡선암호의 키 길이 비교(미국국립표준기술원 권장 키 길이)

대칭 키 크기	RSA 키 크기	타원곡선 키 크기	키 크기 비율	비고
80	1024	160	7:1	취약 강도
112	2048	224	9:1	권장 강도
128	3072	256	12:1
192	7680	384	20:1
256	15360	512	30:1

RSA와 타원곡선암호의 차이점

항목	타원곡선암호 방식	RSA 방식
기반구조	WPKI(무선)	PKI(무선)
속도	빠름	느림
키 크기	상대적으로 작은 키	타원곡선암호에 비해 큰 키
적용	모바일	인프라가 다소 구현된 환경

호환 환경

타원곡선암호 알고리즘을 서버나 운영체제 등에 도입할 때 고려해야 할 조건은 다음과 같다. 만약 조건을 충족하지 못하는 환경에서 타원곡선암호 인증서를 설치할 시, 오류가 발생할 가능성이 있다.

운영체제

이름	최소 버전
애플 맥 OS X 레퍼드	v10.6+
구글 안드로이드	4.0+
마이크로소프트 윈도우	비스타+
레드햇 엔터프라이즈 리눅스	6.5+

서버

이름	최소 버전
아파치	2.2.26+
톰캣	1.1.30+
도브콧	2.2.5+
IBM HTTP 서버	8.0+
NGINX	1.1.0+
자바 시스템 웹 서버	7.0+
윈도우 서버	2008+

라이브러리

이름	최소 버전
바운시 캐슬	1.04+
GnuTLS	2.99.2+
Java JDK	5.0+
NSS	3.8+
OpenSSL	0.9.8b
OpenSSL FIPS Object Module	2.0+

브라우저

이름	최소 버전
애플 사파리	4+
구글 크롬	1.0+
마이크로소프트 인터넷 익스플로러	7+
NSS에 기반한 모질라 제품	3.8+

장점

타원곡선 이론은 대수기하의 한 분야로서 자연스러운 군 연산과 그 연산을 수행해주는 효율적인 알고리즘을 가지고 있어 암호학적 응용이 가능하다. 다른 공개키 암호 시스템과 비교하여 타원곡선 이론의 장점은 다음과 같다.

1. 주어진 유한체 상에서 정의된 다양한 타원곡선을 선택할 수 있다. 주어진 소수 중에서 유한체의 부분 군을 이용하는 것과 대조적인 모습을 통해 풍부한 타원곡선 군을 활용할 수 있는 장점이 있다.
2. 초 특이곡선 같은 특별한 유형의 타원곡선을 제외하고는 알려진 이산대수 문제를 푸는 가장 효율적인 지수계산 알고리즘을 적용할 수 없어 안전한 암호 시스템의 설계가 용이하다.
3. 타원곡선암호는 다른 암호 시스템과 비교하여 짧은 키 길이를 보유하고 있지만 대등한 안정성을 제공하여 높은 효율성을 보여준다.
4. 타원곡선 상의 연산은 유한체의 연산을 포함하기 때문에 하드웨어와 소프트웨어로 구현하기가 용이하다. 모든 사용자가 동일한 유한체와 유한체 연산을 수행하는 같은 하드웨어를 사용하더라도 서로 다른 타원곡선을 선택하여 사용할 수 있으며 추가 보안을 위해 주기적으로 타원곡선을 바꿀 수 있다.
5. 현재 보안 업계에 권장되고 있는 RSA 2048비트와 동일한 암호화 강도를 갖는 타원곡선암호 알고리즘의 길이는 224비트이다. 암호화 강조는 동일하지만 RSA와 비교하여 약 9:1 정도의 길이 감소 효과가 있다. 따라서 사용자 접근이 많은 페이지나 무선 환경과 같은 데이터의 경량화, 고속화가 필요한 환경에 적합하다.

한계점

타원곡선 암호화 기법은 다른 암호화 기법에 비해 높은 효율을 보여주지만 한계점도 분명 존재한다. 그 한계는 구현의 어려움이다. 실제로 비트코인에서 사용된 타원곡선 암호화 기술도 오랫동안 OpenSSL에 기반한 모듈을 사용하다가 최근들어 자체적인 알고리즘으로 바뀌기도 했다. 현재 사물인터넷 기기들의 가장 큰 문제점이 무거운 공개키 기반 구조를 적용하기 어렵다는 부분인데, 타원곡선암호가 이에 대한 해결책으로 언급되지만 이 역시 구현의 어려움으로 지체되고 있다.

블록체인

비트코인 등 블록체인 기반 기술에서는 키 쌍을 생성할 때 타원곡선암호 알고리즘을 사용하며 키 길이는 256비트 이상을 사용한다. 비트코인은 미국 국립표준기술원에서 개발한 secp256k1 표준에 정의된 타원 곡선을 사용하는데, secp256k1 표준에 정의된 타원 곡선 수식은 다음과 같다. 위에서 설명한 타원곡선 암호화 방식에 따라 개인키와 개인키로부터 계산된 공개키를 모두 생성한다.

$y^{2}\,{\bmod {\,}}p=(x^{3}+7)\,{\bmod {\,}}p$

국내 현황

국내에서는 타원곡선암호가 가지는 많은 장점에도 불구하고 구현상의 어려움 때문에 접근이 어려운 상황이었으나 근래에 들어서는 타원곡선 암호기술을 탑재한 CSP(Cryptographic Service Provider) 모듈을 개발하고 타원곡선 암호기술을 접목한 무선 공개키 기반 인증 솔루션을 개발하는 등 한 차원 높은 다양한 보안기술 개발에 주력해오고 있다. 이에 따라 PKI(Public Key Infrastructure) 솔루션업체들은 무선인증시스템 구축을 완료했으며 시범 서비스를 거쳐 이르면 오는 9월 중 상용서비스를 시행할 계획이다. 이 서비스가 시작되면 그동안 무선인터넷 환경에서의 전자상거래 활성화에 가장 큰 걸림돌이던 보안 문제가 해결될 것으로 기대된다. 또한, 무선 시장에서의 경쟁력 확보를 위해서는 타원곡선암호의 상용화 기술의 특허를 피하면서 상호호환성과 함께 보다 효율적으로 구현할 수 있는 고속화 기술 및 최적화 방안에 대한 연구가 요구된다고 볼 수 있다.

참고자료

• 타원곡선 암호 위키백과 - https://ko.wikipedia.org/wiki/%ED%83%80%EC%9B%90%EA%B3%A1%EC%84%A0_%EC%95%94%ED%98%B8
• 타원곡선암호 네이버 지식백과 - https://terms.naver.com/entry.nhn?docId=1232513&cid=40942&categoryId=32204
• 〈타원 곡선 암호화〉, 《토큰 포스트》
• 심경아, 〈(정보보호) 타원곡선 암호시스템 급부상〉, 《한국정보통신기술협회》

• giaysm, 〈타원곡선 암호시스템 급부상〉, 《네이버 블로그》, 2014-12-09
• AEP코리아네트, 〈비트코인에서 사용하는 타원곡선암호기술(ECC)〉, 《네이버 블로그》, 2018-01-05
• ilovemylif, 〈타원곡선암호, Elliptic Curve Cryptography (1)〉, 《네이버 블로그》, 2018-01-17
• 크로커스, 〈타원 곡선 암호학(Elliptic Curve Cryptography)〉, 《크로커스》, 2018-04-10
• 안경잡이개발자, 〈타원곡선암호화 기법(Elliptic Curve Cryptographt)〉, 《네이버 블로그》, 2018-04-28
• 그래비티Grabity, 〈타원곡선 암호과 이더리움 전자서명 ( feat. 우주를 줄게 )〉, 《네이버 블로그》, 2019-03-26
• MIOS Code, 〈ECC, ECDSA 이해하기 (ft. 수학)〉, 《개인블로그》, 2019-06-19

같이 보기

• RSA
• 공개키 암호 알고리즘
• 타원곡선 디지털서명 알고리즘(ECDSA)

이 타원곡선암호 문서는 암호 알고리즘에 관한 글로서 검토가 필요합니다. 위키 문서는 누구든지 자유롭게 편집할 수 있습니다. [편집]을 눌러 문서 내용을 검토·수정해 주세요.

블록체인 : 블록체인 기술, 합의 알고리즘, 암호 알고리즘 □■⊕, 알고리즘, 블록체인 플랫폼, 블록체인 솔루션, 블록체인 서비스 암호기술 개인키 • 경량암호 • 다자간 계산(MPC) • 다중서명(멀티시그) • 동형암호 • 디지털서명 • 링서명 • 배타적 논리합(XOR) • 복호화 • 블랙박스 암호 • 서명 • 소수 • 소인수분해 • 슈노르서명 • 스케인 • 스키테일 • 스테가노그래피 • 안전한 다자간 계산(SMPC) • 암호 • 암호경제학 • 암호문 • 암호키 • 암호학 • 암호화 • 이산로그 • 전자봉투 • 전자서명 • 전치암호 • 종단간 암호화 • 치환암호(대체암호) • 키 • 패딩 • 패스워드 • 평문 • 합성수 • 해독 • 해시 • 형태보존암호 • 혼돈 • 화이트박스 암호 • 확산 논리연산 논리곱(AND) • 논리연산 • 논리합(OR) • 배타적 논리합(XOR) • 부울곱 • 부울대수 • 부울합 • 부정논리곱(NAND) • 부정논리합(NOR) • 부정연산(NOT) SHA SHA • SHA0 • SHA1 • SHA2 • SHA224 • SHA256 • SHA384 • SHA512 • SHA512/224 • SHA512/256 • SHA3 • SHA3-224 • SHA3-256 • SHA3-384 • SHA3-512 MD MD • MD2 • MD4 • MD5 • RIPEMD • RIPEMD-128 • RIPEMD-160 • RIPEMD-256 • RIPEMD-320 기타 해시 CRC-16 • CRC-32 • CRC-64 • Keccak-256 • Keccak-384 • Keccak-512 • Shake-128 • Shake-256 • 베이스32 • 베이스32 파일 • 베이스58 • 베이스64 • 베이스64 파일 • 순환중복검사 대칭키 AES • ARIA(아리아) • DES • HIGHT(하이트) • LEA • SEED(시드) • 대칭키 • 대칭키 암호 알고리즘 • 디피-헬만 • 디피-헬만 키교환 • 레인달 • 블로피시 • 블록암호 • 스트림 암호 • 에스박스(S-Box) • 트리플 DES 비대칭키 PKI • RSA • 공개키 • 공개키 암호 알고리즘 • 비대칭키 • 엘가말 • 타원곡선 • 타원곡선 디지털서명 알고리즘 • 타원곡선암호 영지식증명 영지식 상호 증명(ZKIP) • 영지식 스나크 • 영지식 스타크 • 영지식증명 양자암호 BB84 프로토콜 • E91 프로토콜 • B92 프로토콜 • 비밀키 오류율 • 안전성 증명 • 양자난수생성기 • 양자내성암호 • 양자암호 • 양자얽힘 • 양자역학 • 양자중첩 • 양자컴퓨터 • 양자키 • 양자키분배 • 양자통신 • 연속 변수 프로토콜 암호해독 기지평문공격(KPA) • 선택암호문공격(CCA) • 선택평문공격(CPA) • 암호공격 • 암호문 단독공격(COA) • 암호해독 암호학 인물 라이언 플레이페어 • 레너드 애들먼 • 로널드 리베스트 • 마틴 헬만 • 블레즈 드 비즈네르 • 아디 샤미르 • 앨런 튜링 • 웨슬리 피터슨 • 찰스 휘트스톤 • 휫필드 디피 위키 : 자동차, 교통, 지역, 산업, 기업, 단체, 업무, 쇼핑, 블록체인, 암호화폐, 인공지능, 개발, 인물, 행사, 일반